Big O
알고리즘의 퍼포먼스를 표현하기 위해 사용한다.
괄호 안의 숫자는 inputs의 증가에 따라 연산의 비율이 어떻게 증가하는지를 비율로 나타낸다.
O(1)
주어지는 inputs의 길이가 하나든 둘이든 상관없이 언제나 똑같은 퍼포먼스를 내주기 때문에 O(1)으로 표현한다.
const inputs = [1, 2, 3];
// O(1)
console.log(inputs[0]);
console의 개수는 중요하지 않다.
inputs에 상관없이 동일한 퍼포먼스를 낸다는 점을 봐야 한다.
const inputs = [1, 2, 3, 4, 5, 6];
// O(1)
console.log(inputs[0]);
console.log(inputs[1]);
console.log(inputs[5]);
O(n)
inputs가 길어지는만큼 동일하게 메시지를 출력한다.
n : n과 같으므로 O(n)으로 표현한다.
inputs의 길이가 1이면 1번, 10000이면 10000번 연산한다.
const inputs = [1, 2, 3];
// O(n)
for (let i = 0; i < inputs.length; i++) {
console.log(inputs[i]);
}
아래는 O(2n)으로 표현할 수도 있겠지만 근사치인 O(n)을 쓴다.
const inputs = [1, 2, 3];
// O(n)
for (let i = 0; i < inputs.length; i++) {
console.log(inputs[i]);
console.log(inputs[i]);
}
생각해보면 O(n)이나 O(2n)이나 다를 게 없기 때문이다.
당연히 O(n + 1), 이런 표현도 쓰지 않는다.
O(n^2)
for문에 for문을 쓰면 n x n과 같으므로 n의 제곱으로 표현한다.
const inputs = [1, 2, 3];
// O(n^2)
for (let i = 0; i < inputs.length; i++) {
for (let j = 0; j < inputs.length; j++) {
console.log(inputs[j]);
}
}
O(log n)
알고리즘을 최적화하면 경우에 따라서 O(log n)을 만들 수 있다.
O(log n)은 O(1)과 O(n) 사이의 값으로 Binary Search가 대표적인 예다.
inputs의 길이가 길어질수록 효율이 좋아진다.
O(2^n)
O(n^2)보다 더 심각한 퍼포먼스를 나타내고
O(log n)과 반대로 inputs의 길이가 길어질수록 효율이 똥된다.
이상을 그래프로 표현하면 다음과 같다.
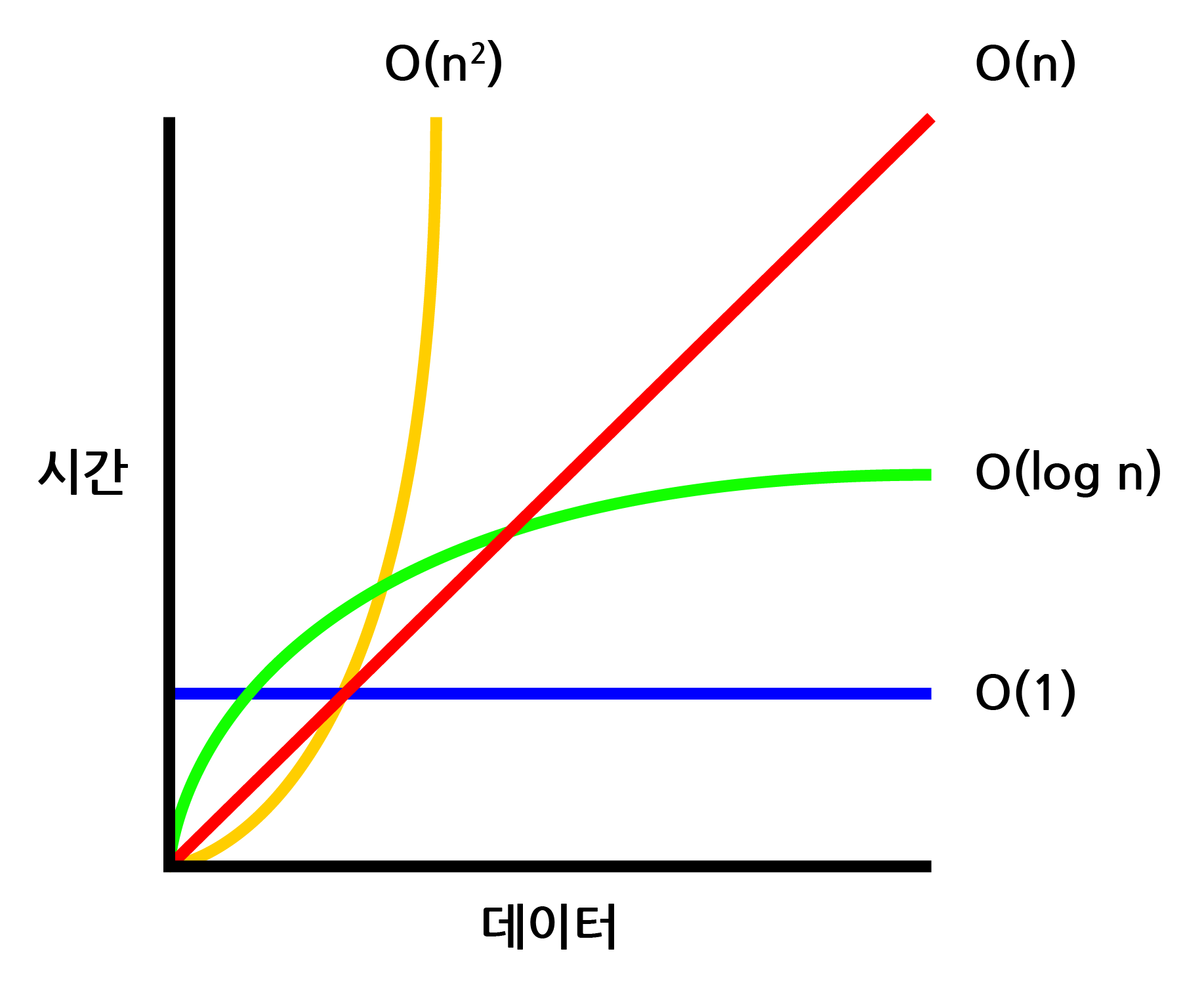
공간 복잡도
보통 Big O라는 표현은 위처럼 연산 속도를 개선하기 위한 목적으로 쓰이지만
메모리와 같은 저장 공간을 최적화 할 때도 쓰인다.
Big O로 연산 속도를 나타내면 시간 복잡도(Time Complexity)가 되고
저장 공간을 나타내면 공간 복잡도(Space Complexity)가 된다.
서버에서 사용하는 슈퍼 컴퓨터가 저장 공간을 고려하는 것은 별 의미가 없지만
모바일이나 임베디드 같은 작은 메모리를 지닌 장치의 경우 저장 공간을 고려하지 않을 수 없다.
다음 예제는 메모리에 하나의 변수를 할당한뒤 숫자를 계속 바꿔서 저장하므로
inputs의 길이가 아무리 길어도 공간 복잡도는 O(1)이다.
// O(1)
const inputs = [1, 2, 3, 4, 5, 6];
for (let i = 0; i < inputs.length; i++) {
console.log(inputs[i]);
}
그러나 inputs을 복사할 경우 inputs의 길이에 따라 배열의 값을 담는 공간도 똑같이 늘어나게 되니
공간 복잡도는 O(n)이 된다.
// O(n)
const inputs = [1, 2, 3, 4, 5, 6];
const copyed = [...inputs]; // copy
for (let i = 0; i < copyed.length; i++) {
console.log(copyed[i]);
}'자료구조와 알고리즘' 카테고리의 다른 글
| 자바스크립트를 예제로 하는 자료구조와 알고리즘 3 - 링크드 리스트(Linked List) (0) | 2021.02.25 |
|---|---|
| 자바스크립트를 예제로 하는 자료구조와 알고리즘 2 - 배열(Array) (0) | 2021.02.24 |
| 알고리즘 어떻게 준비할까? (0) | 2020.07.24 |
| 시간 복잡도 (Time Complexity) (0) | 2020.03.24 |
| 리스트, 해시 테이블, 그래프, 트리 (Linked List, Hash Table, Graph, Tree) (0) | 2020.03.19 |

