1. Linked List
리스트는 데이터가 저장되는 노드에 데이터 필드와 링크를 마련해놓고
데이터 필드에 데이터를, 링크에 다음 노드가 무엇인지를 가리키는 정보를 저장한다.
때문에 정적 배열과 달리 중간의 노드를 삭제하더라도
삭제한 노드의 앞 노드의 링크를 뒤 노드에 연결시켜 단순한 작업으로 데이터를 수정할 수 있다.
노드를 추가하는 것도 마찬가지다.
다만 노드에 두 정보가 들어가니 정적 배열보다 용량이 클 수밖에 없다.
노드에 링크 하나가 있으면 Singly Linked List라고 하고
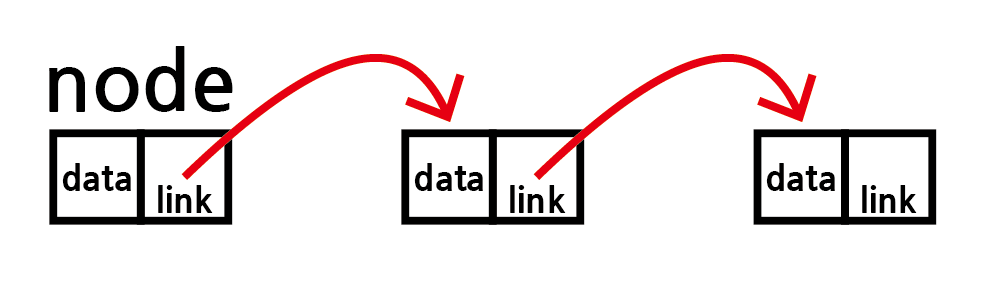
링크가 둘 있으면 Doubly Linked List라고 한다.
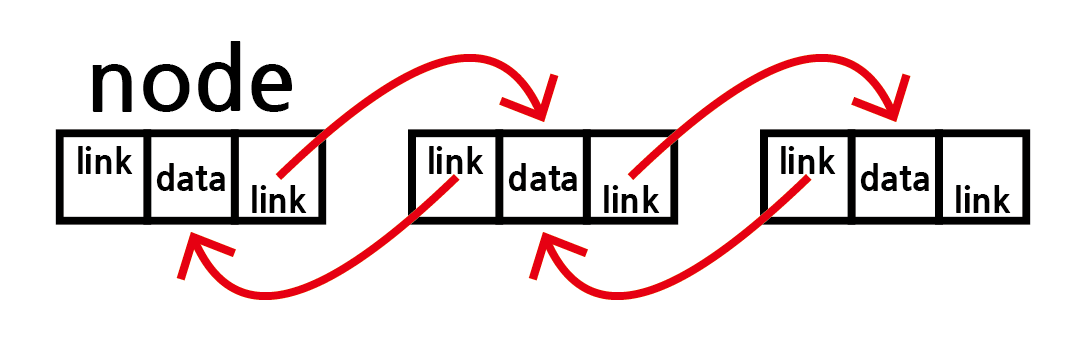
링크가 하나 더 있으면 양쪽 방향으로 움직일 수 있어
성능이 더 좋을 것으로 생각되지만 용량은 더 커진다.
끝 노드의 링크를 첫 노드에 연결시켜
Circular Linked List라는 형태로도 만들 수 있다.
2. Hash Table
해시는 데이터가 들어왔을 때 설정해 놓은 해시 함수에 따라 조건에 맞는 인덱스로 데이터를 보낸다.
데이터를 찾을 때도 해시 함수에 따라 원하는 데이터의 인덱스에 바로 접근할 수 있어 성능이 뛰어나다.
다만 리소스를 많이 차지한다.

위와 같은 테이블을 해시 테이블이라고 하고
인덱싱된 기준을 버킷, 버킷 안에 들어간 값을 엔트리라고 한다.
인덱스에 이미 값이 있으면 Chaining이라는 방법을 써서 리스트처럼 데이터를 이어줄 수 있고
다른 방법으로 Linear Probing이라는 방법을 써서 비어 있는 다음 인덱스에 넣어줄 수도 있다.
만약 Linear Probing을 쓸 때 해시 테이블에 자리가 부족하다면 Resizing을 통해서 늘려줘야 한다.
3. Graph
그래프는 노드와 노드를 이어주는 엣지로 구성된다.
Linked List와 다른점이 있다면 그래프는 노드를 연결해주는 엣지에 제약이 없다,
엣지를 이용해서 모든 노드를 연결할 수 있고 심지어 자기 자신까지도 연결할 수 있다.
노드를 연결해주는 엣지에 방향성이 있으면 Driected Graph라고 부르고
방향성이 없으면 Undirected Graph라고 부른다.
Directed Graph 방식으로 연결하다가 노드 간에 하나라도 원이 형성되면
Cyclic Graph라고 부르고 그렇지 않으면 Acyclic Graph라고 부른다.
그래프를 표현하는 방법에는 2가지가 있다.
Adjacency Matrix는 표형태의 2차원 배열을 만들어서
서로 연결이 되면 1, 그렇지 않으면 0을 넣는다.

Adjacency List는 각 노드를 배열에 넣고
각 노드에 인접한 노드들을 Linked List로 나열한다.
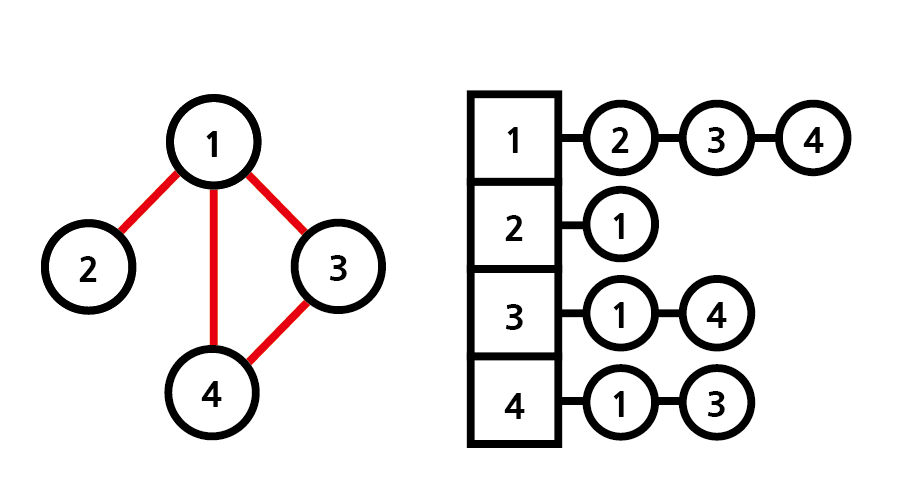
인접한 노드들의 총 개수는 엣지 수의 2배와 같다.
4. Tree
트리는 Directed Graph의 한 종류로 볼 수 있다.
들어오는 엣지는 하나로 하나의 부모만을 둘 수 있고
나가는 엣지에는 제한이 없어 제약 없이 자식을 둘 수 있다.

- Binary Tree
자식을 최대 2까지 가질 수 있는 트리다.
3가지 순회 방법이 있다.
전위순회(preorder), 중위순회 (Inorder), 후위순회 (postorder)
- Binary Search Tree
- AVL Tree
- Red Black Tree
자료 조회와 관련된 키워드
DFS (Depth-first Search) : 깊이 우선 탐색
BFS (Breadth-first Search) : 위에서부터 탐색
'자료구조와 알고리즘' 카테고리의 다른 글
| 자바스크립트를 예제로 하는 자료구조와 알고리즘 2 - 배열(Array) (0) | 2021.02.24 |
|---|---|
| 자바스크립트를 예제로 하는 자료구조와 알고리즘 1 - Big O (0) | 2021.02.24 |
| 알고리즘 어떻게 준비할까? (0) | 2020.07.24 |
| 시간 복잡도 (Time Complexity) (0) | 2020.03.24 |
| 스택과 큐 (Stack & Queue) (0) | 2020.03.19 |


